Tak jsem se opět od plochozemského mistra refrakce a perspektivy, pana Petra StopaSedmilháře Lukeše dozvěděl, jak že tu perspektivu kulatozemci nechápou. Škoda, že nám ji stále nevysvětlil. Už mohly dávno všude viset má videa s omluvou, jen k tomu vysvětlení ze strany Petra Lukeše jako již tradičně nedošlo. No a teď tu máme něco nového...
https://www.facebook.com/share/p/5VZ7Y2BGCEetx5HS/
Na adresu fotografie vrcholu Canigou směrem od Marseille, kde je pod vodní hladinou schováno cca 2500 metrů, nám tento plochozemský odborník tvrdí:
"těch vámi deklarované 2500m bude mít Úhlavou velikost cca půl stupně, možná míň, což je výška několik mm nebo cm. Navíc středové promítání vám nutně opticky nižší úroveň před horami opticky zvedá ke středu pozorovatele. Není to tedy tak působivé překrytí, jak se snažíte říct. Navíc vrchol i slunce by ve vašem modelu byly již pod horizontem a vám nezbývá než se uchýlit k typu refrakce, který jste žel dosud v přírodních podmínkách nebyl schopen potvrdit."
https://flerfies.vanecek.info/panorama/canigou/
"Těch vámi deklarované 2500 m bude mít Úhlavou velikost cca půl stupně, možná míň, což je výška několik mm nebo cm."
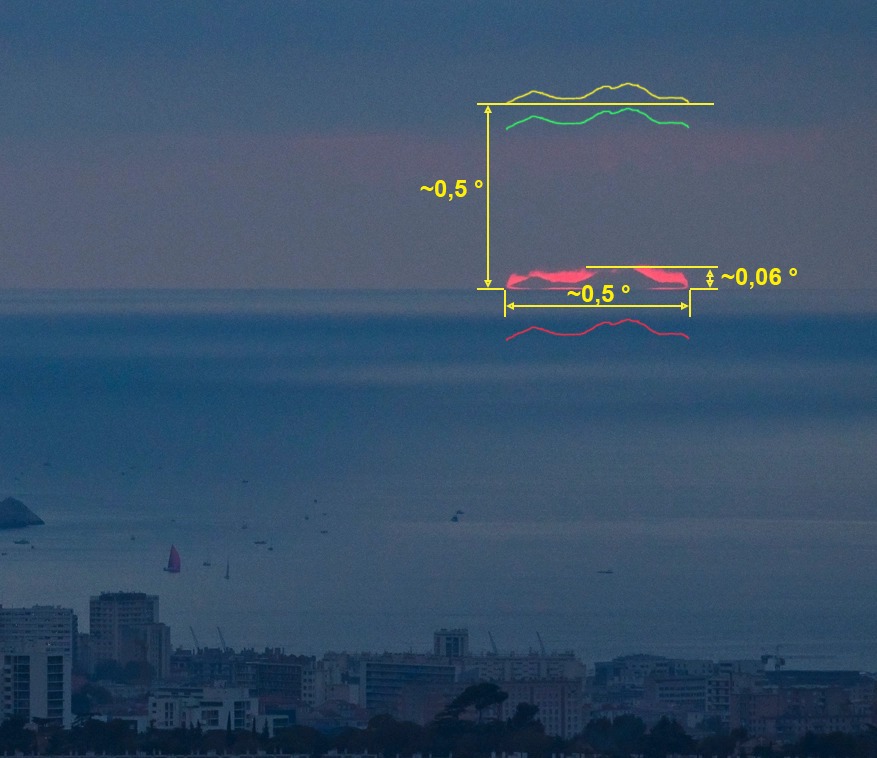
Výborně. Tady nám pan Lukeš nelže a s úhlovou velikostí má celkem pravdu. Je to opravdu cca půl stupně, možná víc, konkrétně 0,54 °. S tou výškou několika mm nebo cm je to už poněkud zavádějícíc, že? O jaké výšce se to pan Lukeš baví? O výšce na snímači fotoaparátu? Použitý Nikon D7000 je APS-C (23.6 x 15.7 mm) s objektivem 300 mm, tedy opravdu to bude maximálně pár milimetrů. Ostatně jako cokoliv, co se na tento (a vlastně většinu běžných fotoaparátů vyfotí). Takže i v tomto případě má pravdu, i když ta informace je nicneříkající. Co je ovšem zajímavé, je těch půl stupně. To je totiž přibližně stejná úhlová velikost, jakou má Slunce, které na fotografii vidíme. To je však podstatně větší, než vrcholky, které koukají nad hladinou, že?

Na obrázku je výřez vrcholů se zapadajícím Sluncem. Slunce má šířku přibližně 190 pixelů, vrcholy jsou asi 22 pixelů nad hladinou. Tedy přibližně 0,06 °. To celkem dobře odpovídá úhlové velikosti 300 metrů (to je to, co je z vrcholů vidět) na vzdálenost 263 km.
Ve skutečnosti by měly být vrcholy na ploché zemi o ten půl stupeň výš, což na obrázku ukazuje ta žlutá silueta.
"Navíc středové promítání vám nutně opticky nižší úroveň před horami opticky zvedá ke středu pozorovatele."
To je opět značně pochybné vyjádření. Třeba už je pro to, že viditelný horizont z výšky 300 metrů není ve vodorovném směru. Ale i když na něj přistoupíme, horizont se údajně na ploché zemi zvedá do úrovně očí. Ta je cca 300 metrů.
Stále by tedy mělo být vidět téměř 2500 metrů z 2785 metrů vysokého vrcholu Canigou (tedy ten půl stupeň - zelená silueta).
"Není to tedy tak působivé překrytí, jak se snažíte říct."
Mně to stále připadá jako dosti působivé. je to několikanásobně víc, než vidíme na fotografii.
"Navíc vrchol i slunce by ve vašem modelu byly již pod horizontem a vám nezbývá než se uchýlit k typu refrakce, který jste žel dosud v přírodních podmínkách nebyl schopen potvrdit."
Tak předně začneme tím, že ani na placce by se to bez refrakce neobešlo. Refrakce by musela zakrýt těch 2500 metrů. Pravdou je, že na kulaté Zemi s poloměrem kolem 6370 km by bez atmosféry nebyl vidět vrchol vůbec. Měl by totiž být asi 390 metrů pod horizontem (červená silueta), ale vidíme z něj asi 300 metrů. Máme tu tedy buď refrakci, která potřebuje ubrat přibližně 0,54 ° v případě ploché země nebo přidat 0,15 ° v případě kulaté Země, tedy u ploché země asi 3,6x víc.
A že to nebyl schopen nikdo potvrdit? Existují desítky měření refrakčních koeficientů v závislosti na nadmořské výšce a tato měření se běžně používají pro další výpočty. Takže tenhle výkřik je čistá plochozemská lež. Jen na mátkou, první dva články, které mi vypadly z vyhledávače:
https://www.researchgate.net/publication/303559426_Correction_of_Atmospheric_Refraction... https://onlinelibrary.wiley.com/doi/10.1155/2020/2438515
Co je však na této fotografii zajímavé je fakt, že byla pořízena 1. listopadu během západu Slunce (tedy přibližně 16:30 UTC). Podle slavné a plochozemci uznávané Gleasonovi mapy by tou dobou mělo být Slunce o více jak 20 stupňů napravo.
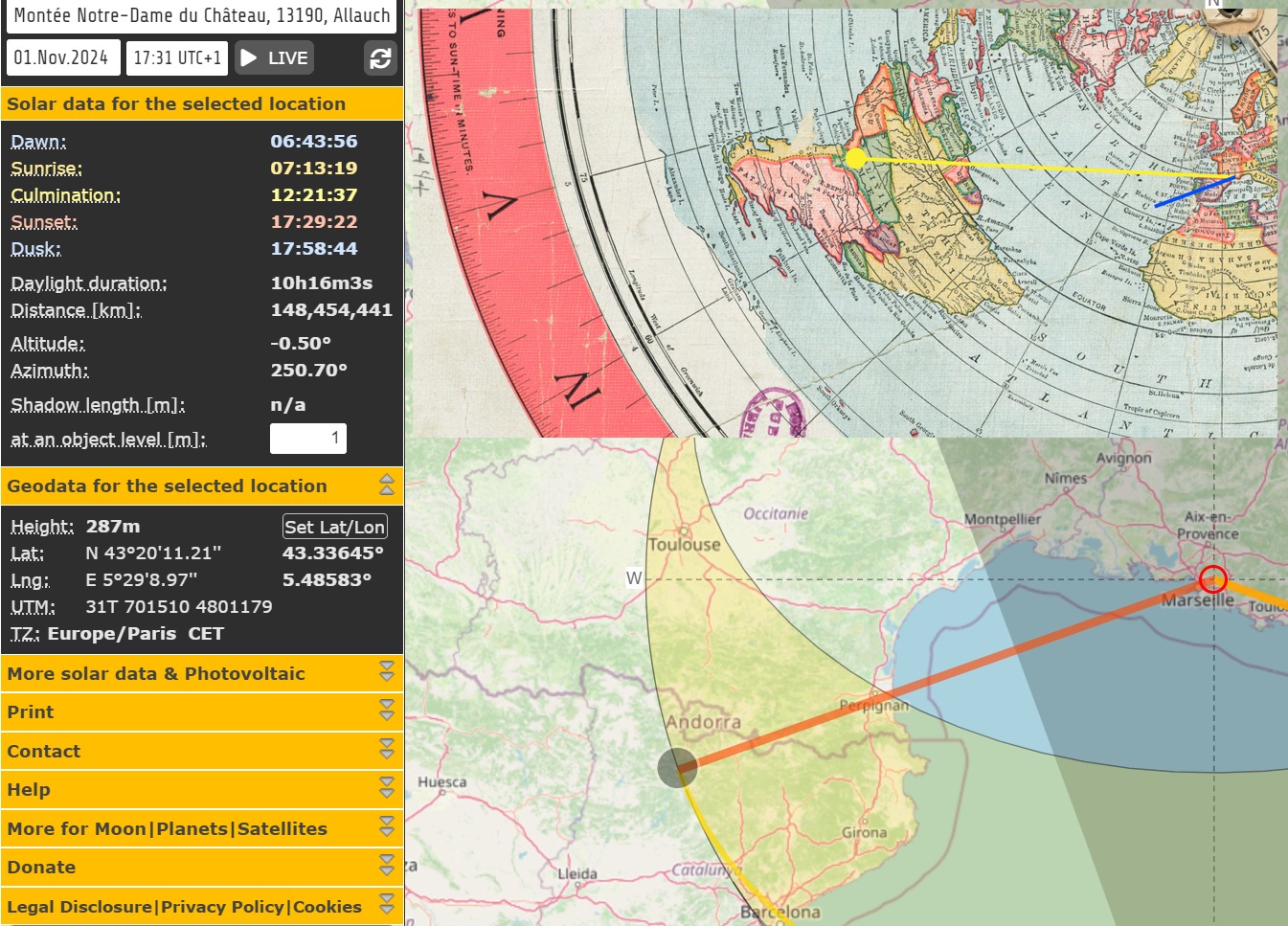
Působí snad plochozemská refrakce i do stran? A to o takový úhel? Co na to Petr Lukeš? Podařilo se nějakému z plochozemců prokázat takové chování v přírodních podmínkách?