Ztracené kameny (1250 m n. m.) je skalní útvar asi 8 km jihozápadně od Pradědu. Na kanále uživatele Stopa7 je video, s pohledem na Tatry, konkrétně na oblast kolem Lomnického štítu (2634 m n. m.) ve vzdálenosti 237 km (mapa).
Pro výpočet výškového profilu byla použita stránka Hey Whats That. V případě ploché země by kopce v okolí Kýčery měly být podstatně níž (nachází se pod horizontální osou pohledu). Po cestě by nad horizontální osou pohledu měla být vidět celá řada dalších vrcholů (mj. Krokiew 1378 m) a jiné vrcholy podstatně výš (Mala Koszysta 2014 m, na videu nesprávně označena jako Svišťovky). Pro kulatou Zemi není nastavena žádná refrakce, Lomnický štít je viditelný, o něco bližší Svišťovky/Koszysta (2070/2014 m n. m.) jsou však schované.
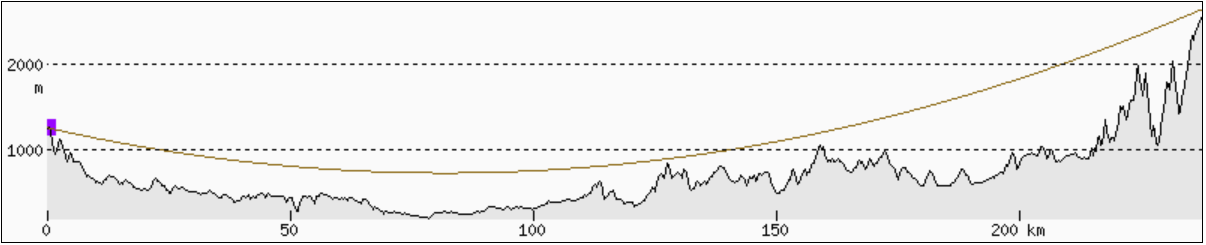
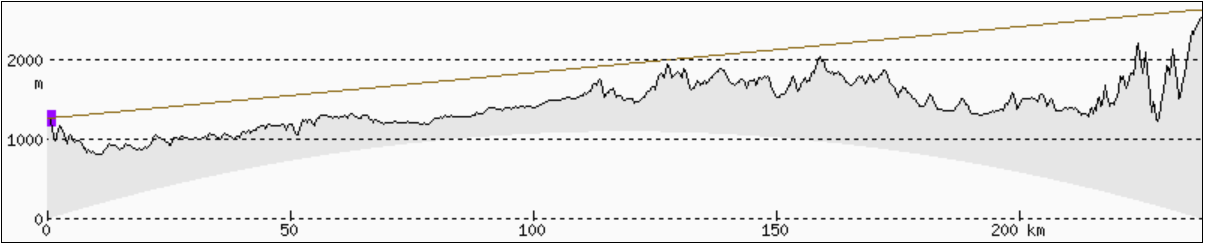
Simulovaný pohled (U. Deuschle) poměrně dobře odpovídá, pokud se výška posune do 1270 m n.m. (tedy necelých 20 metrů na 230 km, tedy změna o méně než 0,01 %). Částečně to může být způsobeno tím, že není známá úplně přesná poloha, odkud byl snímek pořízen.
(Po najetí myší na obrázek se model překryje fotkou z videa.)
Pro porovnání ještě uvádím, jak vypadá obrázek z videa (uprostřed), vlevo jak by situace vypadala na kulaté zemi s průměrnou refrakcí a vpravo jak by situace vypadala na placaté zemi (po kliknutí se otevře obrázek v plném rozlišení).
Z celé fotografie lze vyčíst poměrně dost informací. Začněme tím, že se pokusíme určit ohniskovou vzdálenost fotoaparátu. Mám k dispozici pouze video a předpokládám, že není nějak oříznuté. Na základě úhlu, který svírá Kolový a Malý Ľadový štít od Ztracených kamenů (cca 0,47°) můžeme z videa zjistit, že celkový horizontální úhel je něco málo nad 1° (vyšlo mi přibližně 1,07°). To by vycházelo na ohniskovou vzdálenost někde kolem 1930 mm, což by mohlo poměrně dobře odpovídat oblíbenému plochozemskému kompaktíku Nikon P900 (díky jeho miniaturnímu chipu by jeho objektiv 357 mm vcelku odpovídal).
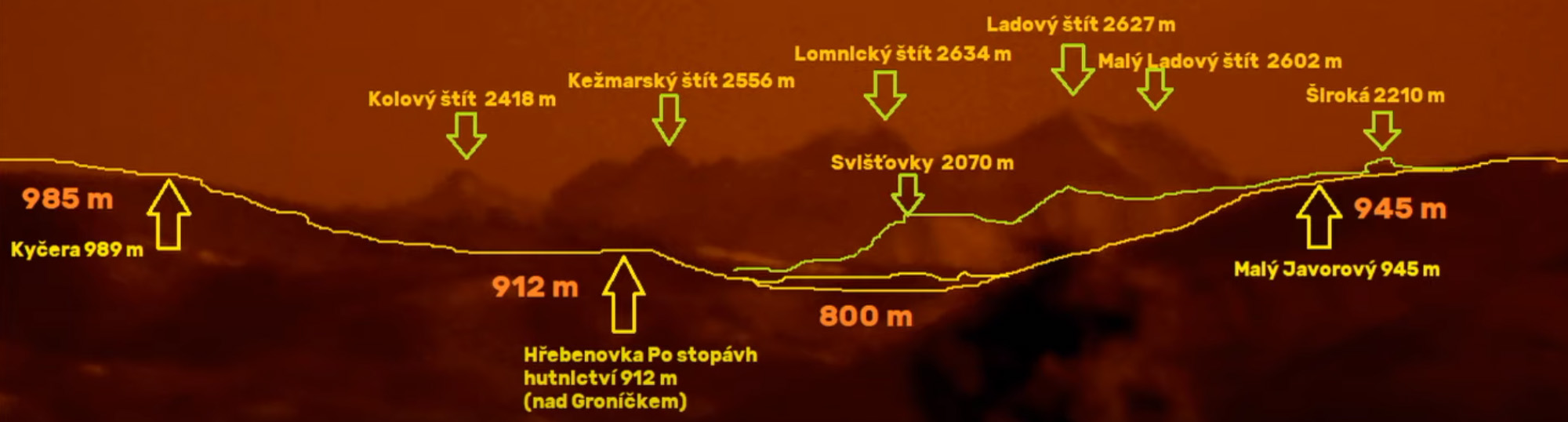
Na snímku z videa jsou vyznačena místa, pro která se počítají úhly (tedy Okrouhlík, Malý Javorový, Široká Veža).
Po cestě od Ztracených kamenů (1250 m n.m.) k Široké Veži (2461 m n.m.) máme celkem dost dobře identifikovatelných bodů viz mapa. Z nich bych vybral ty, které jsou dobře viditelné na videu. Konkrétně hrana ve vzdálenosti cca 60 km (Okrouhlík 467 m n.m.), která je těsně pod spodní hranou videa při nejvyšším přiblížení, dále svah Malého Javorového (cca 900 m n.m.) a nakonec samotná Široká Veža. Nad 1250 m n.m., tedy nad výškou Ztracených kamenů a nad výškou Malého Javorového, který je v tomto směru dominantním vrcholem nevidíme na videu např. následující vrcholy: Turnia Kiernia (vzdálenost 215 km, výška 1316 m n.m.), Małe Uhrocie Kasprowe (vzdálenost 220 km, výška 1750 m n.m.), Żółta Turnia (vzdálenost 223 km, výška 2087 m n.m.). Jak je to možné?
Díky tomu, že známe ohniskovou vzdálenost, můžeme z videa určit úhly mezi Okrouhlíkem a Malým Javorovým (cca 0.34°) a Malým Javorovým a Širokou Věžou (0.017°). Odhady je třeba brát velmi s rezervou kvůli kvalitě obrazu, je ale celkem zřejmé, že úhel Malý Javorový - Široká Veža je přibližně 20x menší než úhel Okrouhlík - Malý Javorový. Nyní můžeme spočítat, jaké jsou úhly na ploché a na kulaté zemi.
Budu počítat úhel od vertikální osy směrem dolů, nebudeme tak muset řešit, kde má být horizont. Pro plochou zemi můžeme snadno spočítat úhel k Okrouhlíku (vzdálenost 62 km, výška 467 m) - 89,276°, K Malému Javorovému (vzdálenost 113 km, výška 900 m) - 89,823° (Okrouhlík - Javorový tedy 0,547°) a k Široké Veži (vzdálenost 235 km, výška 2461 m) - 90,271° (Javorový - Veža tedy 0,448°). Na ploché zemi tedy vychází úhly takřka srovnatelné, určitě ne 20x menší.
Stejný výpočet můžeme udělat na kulaté Zemi. Na způsobu výpočtu se můžeme domluvit. Pro začátek třeba velmi zjednodušeně posunu všechny vrcholy po cestě o odpovídající "pokles" podle vzdálenosti. Pokud v tomto zjednodušení vidíte zásadní problém, můžeme celou věc vypočítat jinak (např. použít vzdálenosti po oblouku a výšky kopců upravit podle jejich odklonu od počáteční svislé osy). Pro pokles použiju https://earthcurvature.com. K Okrouhlíku (467 - 302 metrů) je úhel 88,997°, k Javorovému (900 - 1002 metrů) je úhel 89,315° (rozdíl 0,318°), k Veži (2461 - 4334 metrů) je úhel 89,239° (rozdíl -0,076°). Bez započítání refrakce tedy nebude na kulaté Zemi Široká Veža vidět o cca 0,076° (potřebujeme tedy změnu cca o 0,1° oproti videu). Naproti tomu v případě ploché země budeme potřebovat korekci větší než 0,4°.
Obrázky profilu z http://heywhatsthat.com nemají shodné jednotky v ose X a Y, ale jak jsem pochopil z plochozemských videí, to by neměl být problém. Důležité je, že výpočet není z těchto grafů, ale z reálných vzdáleností a nadmořských výšek. Modré úsečky označují postupně místa Okrouhlík (62 km), Malý Javorový (113 km) a Żółta Turnia (223 km). Zelená čára na profilu ploché země označuje vodorovný pohled v výšce 1250 m. Červené úsečky spojují pozorovatele u Ztracených kamenů s jednotlivými místy.
Ještě je tu taková drobnost. Vertikální zorný úhel při dané ohniskové vzdálenosti bude někde kolem 0,69°. Na ploché zemi je ale zorný úhel od Okrouhlíku po Širokou Vežu téměř celý stupeň. Při největším přiblížení by se tedy scéna nevešla do obrazu.
Ale refrakce přece nevytahuje objekty schované za překážkou! Vážně? Pravdou je, že refrakce, která se běžně ukazuje ve škole pomocí optických prvků (typicky přechod ze vzduchu do skla) to skutečně neumí. Ke zlomení paprsku dochází pouze na rozhraní dvou různých optických prostředí. Atmosféra ale není homogenní prostředí. Se vzrůstající nadmořskou výškou klesá její hustota (tomu věří dokonce i většina plochozemců). K refrakci tedy dochází průběžně, což má za následek ne zlomení paprsku, ale jeho ohyb.
To lze v menším měřítku ukázat i v jiném nehomogenním prostředí - např. ve vodě s různou hustotou. Jak to vypadá se můžete podívat třeba tady.
Použité fotografie jsou z YouTube kanálu Stopa7, ostatní obrázky buď ze zmíněných nástrojů, nebo moje vlastní.
Protože podle Petr Lukeš je kolega Vaněček idiot, rád bych tímto pana Lukeše požádal, aby do obrázku dokreslil, jak tedy přesně funguje perspektiva a jak je možné, že ze Ztracených kamenů (1250 m) přes Malý Javorový (945 m, nebudeme řešit, že to je navíc přes svah a ne přes vrchol) není vidět kopce, vyznačené na obrázku červeně. Z vrcholu Široká veža (2461 m) je pak přes Malý Javorový vidět pouze nepatrný kousek.
Jak jsem slíbil, zde jsou dokreslené obrázky pana Lukeše. Podle nich, z ploché země skutečně nemůžeme dostat stejný obraz, jako je na jeho fotografii. Jinak ponechávám bez komentáře. Další povídání o plochozemské perspektivě je na samostatné stránce.
