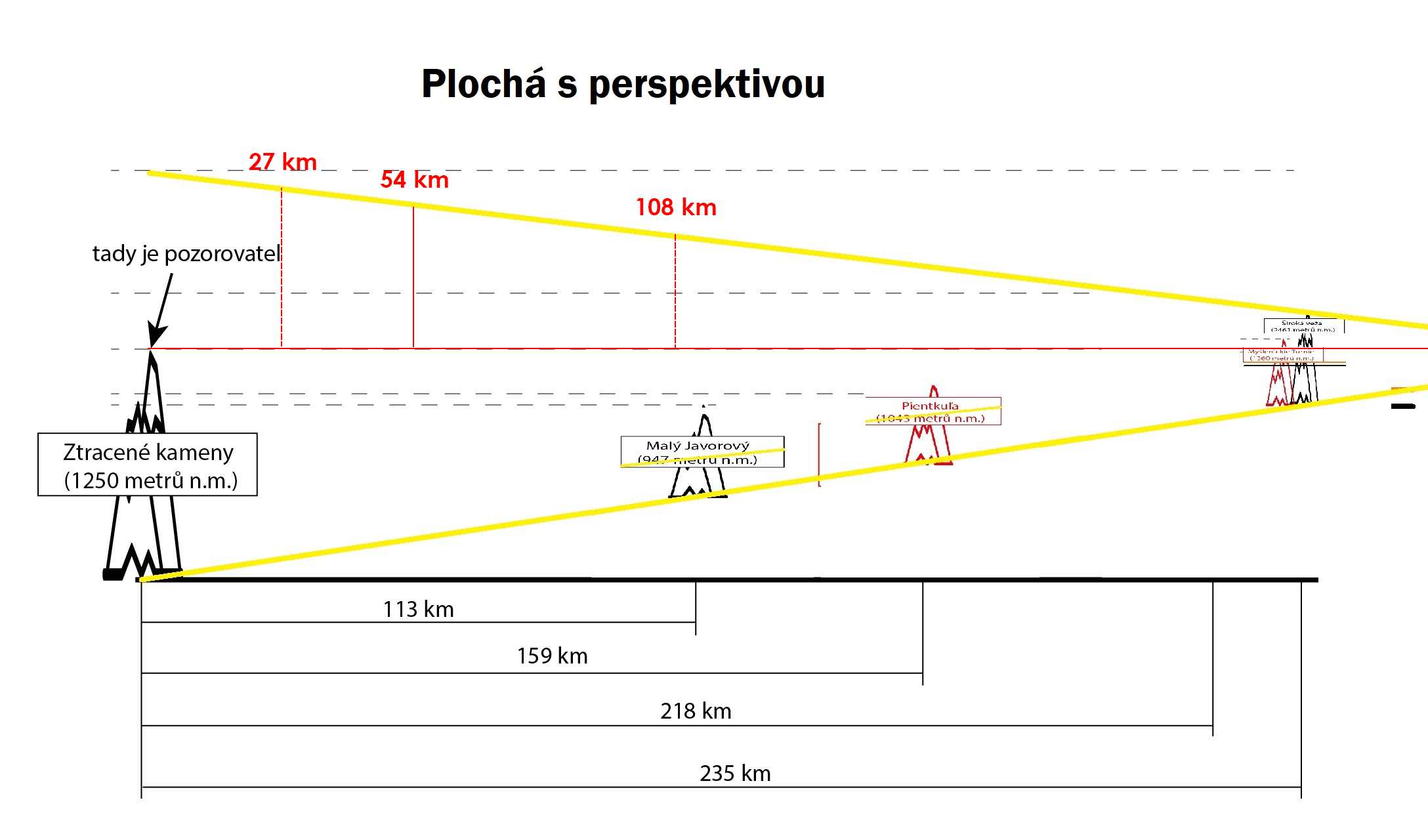
V debatě z úst profesora plochozemské perspektivy Petra Lukeše opět zaznělo, že kulatozemci nerozumí perspektivě a že ji zakreslují chybně. Ani přes několik výzev, aby nám tedy přesně ukázal, jak má ta perspektiva vypadat, to nikdy pan Lukeš nezvládl a z každé takové výzvy statečně utekl. No a podobně jako třeba jeho výzva na natočení refrakce, která vytahuje objekty za překážkou (kdy tvrdil, že v akváriu s vodou o různé optické hustotě k ničemu takovému nedochází: video), tak i tady jsem se rozhodl, že tu perspektivu tedy nakonec nakreslím sám.
Vycházím z toho jednoduchého principu (na který se pan Lukeš odkazuje), že dvakrát vzdálenější objekt se nám jeví 2x menší. Už tady ovšem vše naráží na absolutní nepochopení základoškolské matematiky z jeho strany viz jeho obrázek, kdy ty jeho žluté úsečky tuto vlastnost nesplňují. Do obrázku jsem domaloval vzdálenost 27, 54 a 108 km. Podle perspektivy by ale žlutá čára měla být na 54 km v poloviční oproti 27 km a taktéž na 108 km by měla být v poloviční výšce oproti 54 km. Tak to alespoň pan Lukeš říká.

Pojďme se tedy podívat na ty jeho slavné Tatry, ve kterých o ničem nelže (lží je tam hned několik) a které prý kreslíme blbě, protože zanedbáváme perspektivu (ukážeme si, že geometrie je natolik krásná a konzistentní, že je úplně jedno, jak danou situaci zakreslíme, pokud to děláme správně). Pro připomenutí, obrázek z videa Petra Lukeše, vyznačil jsem na něm 113 km vzdálený 947 metrů vysoký Malý Javorový a za jeho svahem, ve výšce asi 900 metrů se ve vzdálenosti 236 km schovává 2462 metrů vysoká Široká veža. Fotografie je pořízena nad Ztracenými kameny, ve výšce kolem 1250 metrů (tedy nad 300 metrů nad vrcholkem Malého Javorového).

Kromě výše zmíněných jsem po cestě mezi pozorovatelem a Širokou vežou vybral některé další vrcholy ležící přibližně ve směru pohledu (viz tabulka).
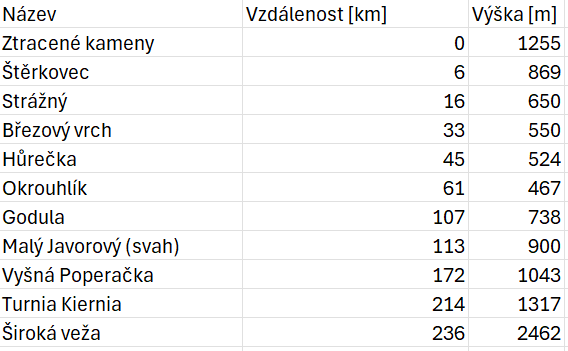
Pojďme tedy na to plochoperspektivení... Je třeba zvolit nějaký referenční kopec, vůči kterému budeme následně ty poměry počítat. Profesor Lukeš sice neustále zmiňuje, že kopec na kterém stojím (tedy vzdálený 0 km) je vysoký tolik a tolik, takže kopec ve dvojnásobné vzdálenosti bude poloviční... Většina lidí se základním vzděláním ten nesmysl vidí - 2 x 0 je stále 0 pane Lukeši. Takhle to fungovat nebude, že? Pokud nevěříte, vemte si libovolně dlouhou tyč, zavřete jedno oko, podívejte se kolmo vzhůru a přesně do osy pohledu umístěte tu tyč. Nyní řekněte, jak je dlouhá. To půjde asi dot těžko, že, když vidíte pouze její podstavu.
Takže referenční kopec, který je libovolně vzdálený od pozorovatele - vybral jsem 6 km vzdálený Štěrkovec (na fotografii vidět není, ale stejně tak lze vybrat libovolný jiný kopec). S každým zdvojnásobením vzdálenosti se žlutá čára umístěná do 500 metrů od výšky pozorovatele (tedy 1755 a 755 metrů) přiblíží na poloviční vzdálenost k ose pohledu (volil jsem tečnu k povrchu ve výšce 1255 metrů).
Přesný zorný úhel lidského oka je trochu ošemetná záležitost z mnoha důvodů. Běžně se ale počítá s tím, jak velký zorný úhel dokážeme najednou zaostřit (centrální vidění) a to odpovídá přibližně 40 - 50°. To odpovídá ohniskové vzdálenosti objektivu někde kolem 55 mm, což při přepočtu na kinofilm 35 mm odpovídá přibližně právě tomu lidskému zraku. Vertikálně pak 55 mm odpovídá na kinofilmu přibližně 29° (poměr výška:šířka kinofilmu je 36:24, tedy 3:2).
Při této ohniskové vzdálenosti bude 6 km vzdálený 1000 metrů vysoký objekt (500 metrů pod a 500 metrů nad osou) zabírat přibližně 9,5°, tedy něco málo přes 1/3 obrazu. Ve 12 km to bude 4,8°, v 24 km 2,4°, atd. V 85 km to bude 0,67° (vrátíme se později) a ve 200 km to bude pouhých 0,28°, což je přibližně polovina velikosti Měsíce na obloze.
Můžeme celou křivku vynést do grafu a můžeme odpovídajícím poměr přepočítat velikosti vybraných vrcholů. Tento přístup je relativně pracný a pokud se budeme chtít přesunout někam jinam, můžeme celou věc vzít a zahodit. Moc praktická tedy z tohoto pohledu toto zakreslení perspektivy není. Z grafu vidíme, že lidským okem toho moc nevidíme...
Můžeme dokonce vynést jednotlivé vrcholy či celé siluety do obrázku.
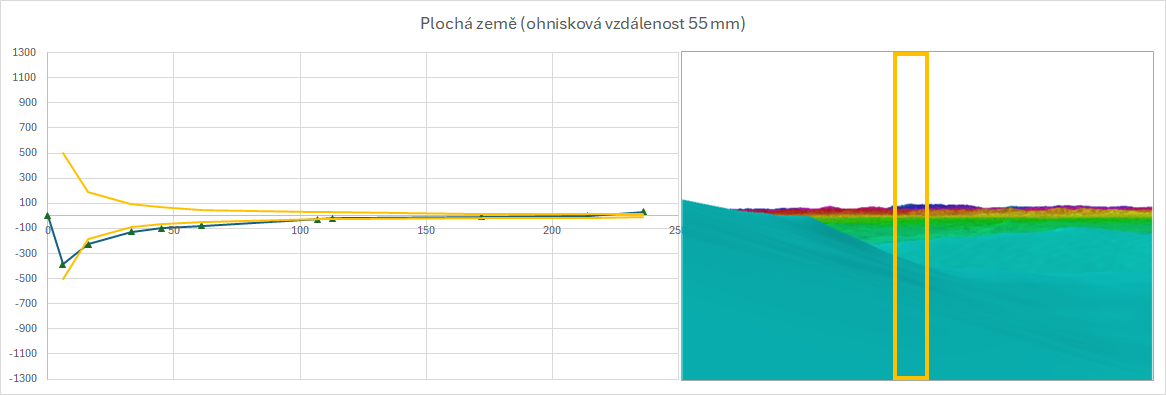
Plochozemci často operují různými superzoomy, aniž by moc tušili, co že to vlastně znamená. To teď ponechám stranou. Fotografie (video) Tater byly pořízeny Nikonem P900, pokud se nepletu. Ten má ohniskovou vzdálenost 357 mm.
"Nené! 2000!" volali plochozemci
Inu, je to tak. 357 mm je ohnisková vzdálenost tohoto slavného přístroje. Jak došlo k těm 2000 mm? Snadno. Ohnisková vzdálenost se pro lepší orientaci (zvláště u výměnných objektivů) přepočítává právě na kinofilm. Jenže Nikon P900 nemá senzor velikosti kinofilmu, tedy 36x24 mm. Má senzor podstatně menší - konkrétně 6,17 x 4x55 mm. To s sebou přináší nějaké klady a nějaké zápory, ale o tom jindy. Pro nás to znamená, že tento titěrný senzor zabírá podstatně menší úhel, čímž se po přepočtu dostáváme právě na nějakých těch 2000 mm. 2000 mm pak odpovídá přibližně 0,69°.
Co znamená změna ohniskové vzdálenosti pro náš graf? Znamená, že z něj jen vezmeme podstatně menší výřez. Naše body 500 metrů nad a pod osou pohledu se do zorného pole takového objektivu dostanou až ve vzdálenosti cca 85 km (říkal jsem, že se k tomuto číslu ještě dostaneme).
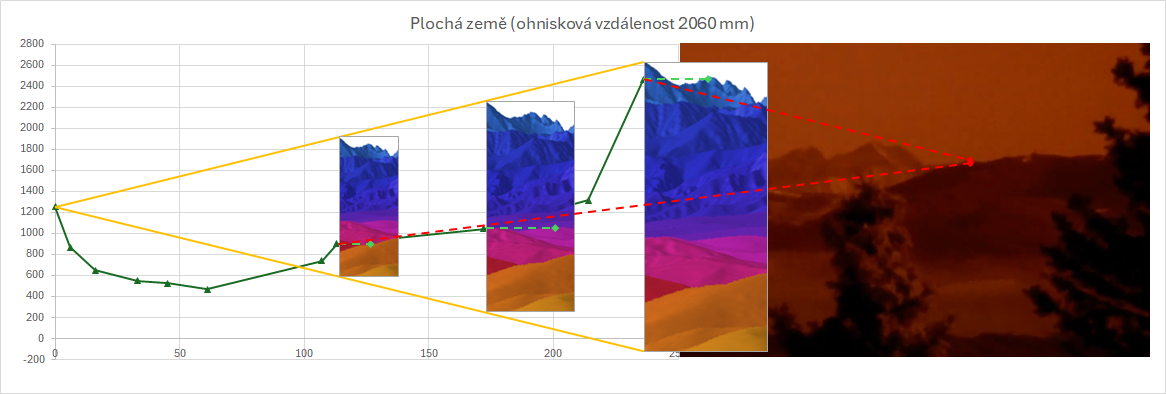
Takže teď můžeme graf pěkně roztáhnout a můžeme znovu nakreslit jednotlivé vrcholy.
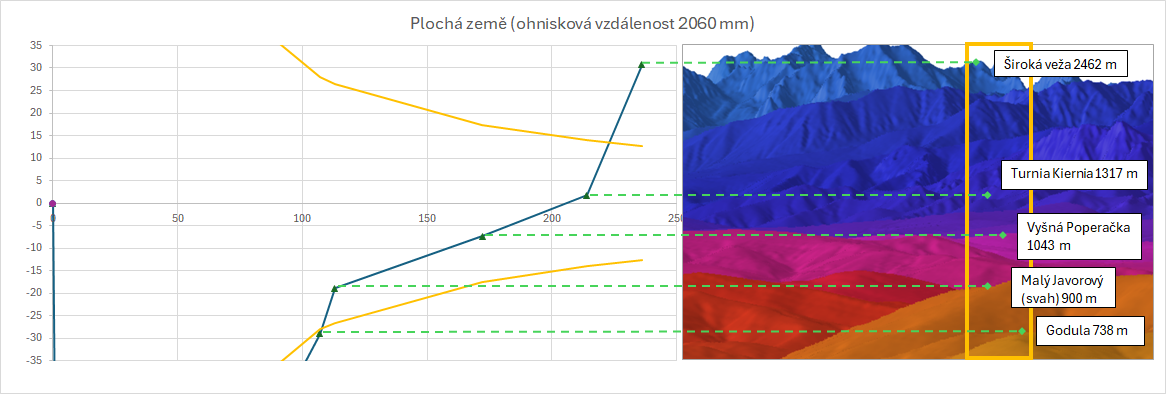
Nevím, jak vám, ale mně nějak přijde, že pokud vynesu výšky vrcholů podle ploché země, moc se nám to s tou fotografií neshoduje, co říkáte? Široká veža, která na fotograafii jen tak tak vykukuje nad svah Malého Javorového, se nyní tyčí vysoko nad ním.
Kulatozemci jsou z podstaty líní tvorové, takže se snaží nepřidělávat si práci. Místo toho, aby při každé změně pozice pozorovatele všechno kreslili pěkně od nuly, jako pečliví plochozemci, nakreslí celou scénu pěkně v měřítku, bez nějakého přepočítávání. Potom stačí pouze píchnout kamkoliv do obrázku, od pozorovatele nakreslit dvě polopřímky s odpovídajícím zorným úhlem a poměry mezi těmi polopřímkami a výškou vrcholů ukazují, kde na fotografii budou vrcholy znázorněny. Pokud se tedy chceme podívat na Malý Javorový, koukáme se, jak to vypadá ve vzdálenosti 113 km, pokud na Širokou vežu, koukáme, jak to vypadá ve 236 km.
No a jak jsem slíbil, geometrie je krásná a je jí úplně jedno, jestli to zakreslíme tak či mak, výsledek je stejný. Výšky vrcholů jsou oběma způsoby na hony vzdálené tomu, co vidíme na fotografii. Děkujeme panu Lukešovi za krásný plochozemský důkaz, že minimálně mezi Českem a Slovenskem, není Země placka s kopci, ale něco prohnutého - třeba část kulového povrchu?
Pro zvědavé přihodím ještě pár odkazů:
https://flerfies.vanecek.info/panorama/ztracene_kameny/
https://flerfies.vanecek.info/perspektiva/
https://flerfies.vanecek.info/vypocty/perspektiva/